
In this article I describe the DEFLATE algorithm that GZIP implements and depends on. The DEFLATE algorithm uses a combination of LZ77, Huffman codes and run-length-encoding; this article describes each in detail by walking through an example and developing source code to implement the algorithm. My aim is to implement readable rather than efficient or extensible code. I'll focus here on unzipping, rather than zipping, but by the end of the article, the zipping process should be clear.
Material intended for human consumption tends to be highly redundant, from an information processing perspective. Because of the mysterious human mind, we need to have the same thing repeated to us in different ways in order for it to be processed correctly. Natural language, for example, is inefficient - the English language phrase "I am going to the store" could easily be abbreviated "I go store". If the subject of conversation has already been established as "me", it could be further abbreviated unambiguously as "go store". This is how children communicate until they are taught proper grammar - but as we mature, we like/want/need the redundancy.
Computers are no better when it comes to demanding redundancy. Computer programs repeat the same instructions over and over again, and program source code is verbose, even when the programmer isn't concerned about using readable variable names (you know who you are). Computer storage, on the other hand, is a scarce resource. It becomes less and less scarce every day, but every time capacity increases, we seem to find a way to run out of it. I'm sure that someday, my children will be complaining that their thumbnail computer devices can "only store four holodeck simulations!"
Computer scientists have been studying ways to use computer storage more efficiently since the 1960s. In 1977, Abraham Lempel and Jacob Ziv published "A Universal Algorithm for Sequential Data Compression " [1] which described what is now referred to as the "LZ77" compression algorithm. Conceptually, LZ77 is pretty straightforward - read the source document, and, for each sequence of bytes encountered, search backward through the document to see if the same sequence occurs previously. If so, rather than outputting the sequence, output a back pointer to the first occurrence of the sequence.
To get a sense of just how redundant English text is, take a look at figure 1 and figure 2. Figure 1 contains the first few verses of the Bible's book of Genesis and figure 2 shows all of the places where text from a prior point in the document is repeated. LZ77 does a very good job of exploiting that redundancy and making efficient use of available storage.

Figure 1: Uncompressed ASCII text

Figure 2: LZW compression
The first 17 verses, with LZ77 compression applied, is shown below. The <#,#> brackets indicate backpointers in the form <distance, length>. So, the first backpointer <25,5> indicates that, to uncompress the document, search backward 25 characters, and reproduce the five characters you find there. As you can see, the first sentence is mostly uncompressed, but by the middle of the text, there's almost no uncompressed text.
001:001 In the beginning God created<25, 5>heaven an<14, 6>earth. 0<63, 5>2 A<23, 12> was without form,<55, 5>void;<9, 5>darkness<40, 4> <0, 7>upo<132, 6>face of<11, 5>deep.<93, 9>Spirit<27, 4><158, 4>mov<156, 3><54, 4><67, 9><62, 16>w<191, 3>rs<167, 9>3<73, 5><59, 4>said, Let<38, 4>r<248, 4> light:<225, 8>re<197, 5><20, 5><63, 9>4<63, 11>w<96, 5><31, 5>,<10, 3>at <153, 3><50, 4>good<70, 6><40, 4>divid<323, 6><165, 9><52, 5> from<227, 6><269, 7><102, 9>5<102, 9>call<384, 7><52, 6>Day,<388, 9><326, 9><11, 3><41, 6><98, 9>N<183, 5><406, 10><443, 3><469, 4><57, 8>mor<15, 5>w<231, 4><308, 5>irst<80, 3>y<132, 9>6<299, 28>a<48, 4>mamen<246, 3><437, 6>midst<375, 7><134, 9><383, 6><177, 6>le<290, 5><272, 6><413, 11><264, 10><429, 15>7<129, 9>mad<166, 9><117, 6><82, 6><348, 11><76, 8>which<215, 5><600, 10>nder<62, 14><115, 16><54, 11> ab<599, 3><197, 13><54, 9><470, 6><487, 7>so<169, 9>8<432, 20><108, 10>H<827, 5><397, 25><103, 9><405, 17>seco<814, 5><406, 10>9<406, 22><199, 8><235, 10><944, 7><428, 3>ga<439, 5><540, 10>toge<18, 4><45, 3>to one pl<820, 3><422, 10><604, 5>ry l<16, 4>app<981, 3><250, 8><474, 11><258, 12>10<258, 20><67, 9>E<1046, 4>;<638, 9><145, 6><234, 4><138, 8><86, 9><952, 13><75, 8><1018, 4>eas<853, 10><894, 6><883, 14><138, 9>1<290, 23><1179, 6>b<119, 5><1173, 3><11, 3>grass,<302, 7>rb<132, 9>yield<38, 4>seed<879, 10>fru<111, 3>tree<33, 10><19, 6>af<174, 3> hi<1229, 10>kin<57, 3>whose<69, 5> is<809, 4>itself,<1260, 10><148, 5><599, 23>1<1367, 16>brou<1082, 5><189, 12><58, 4><189, 4><181, 14><136, 9><154, 9><146, 7><204, 8><198, 19><175, 13><138, 4>i<1369, 10><184, 8><78, 14><401, 39>3<1160, 42>thir<753, 13>14<1460, 33>s<1155, 8><882, 10><1159, 15><780, 7><749, 3><1150, 11><100, 3><1031, 10>n<72, 4>;<769, 12>m<95, 4><361, 3><68, 9>sign<367, 7><22, 3><293, 3>aso<16, 12><79, 3><13, 7>y<430, 3>s:<192, 8><1486, 6><85, 15><185, 31><177, 10><126, 9>giv<1541, 8><573, 38>6<1343, 15>wo<562, 3><2001, 3><122, 7>;<906, 6><2019, 5><142, 7><288, 4>rul<1277, 14>d<1650, 12>l<1646, 3><45, 20><319, 6>:<937, 4><1452, 9>st<261, 3><647, 10>l<154, 11><1498, 10>s<278, 8><264, 33><256, 11><2099, 18><264, 5>,
Example 1: LZ77 compressed representation of the first 17 verses of Genesis
This relatively short document is compressed at just over 3:1 - and the compression ratio generally improves as documents get longer.
Of course, when discussing computer formats, it's not enough to talk about concepts - a concrete representation must be agreed upon. The decoder/decompressor must have a way to distinguish which input bytes are literals, and which input bytes are backpointers. One simple, naive representation might be to introduce an "escape code" - say, 0x255, to distinguish backpointers from literals. Of course, a literal escape code would need to be similarly escaped.
Unfortunately, all of these escape codes end up defeating the purpose of compressing in the first place. As it turns out, there's a better way to encode these backpointers and still allow them to be correctly distinguished from literals: variable length codes. In ordinary byte-oriented data, each code is a fixed length (typically 8 bits). Variable length codes remove this restriction. Some codes can be shorter and some can be longer. Once there's no need to restrict yourself to eight-bit bytes, you can define an arbitrarily-sized "alphabet", which is exactly what GZIP does. The first 255 characters in this alphabet are the literal codes - the 8-bit bytes that were read from the input stream. The 256th character is a "stop code" that tells the decode when to stop decoding. The 257-285th codes indicate the length of the matched range (followed immediately by a distance code).
Now, if there are only 285-257=28 length codes, that doesn't give the LZ77 compressor much room to reuse previous input. Instead, the deflate format uses the 28 pointer codes as an indication to the decompressor as to how many extra bits follow which indicate the actual length of the match. This logic is complex but important for compatibility; I'll cover it in more detail below.
In a fixed-length world, this 285-symbol alphabet would require 9 bits per symbol, but would use only a little more than half of the available 512 bytes that 9 bits can encode. This alphabet can be encoded much more efficiently by assigning the symbols variable-length codes. However, the problem with variable length codes is that the decoder needs to know where one code ends and the other begins. This isn't a problem with fixed-length codes such as ASCII - the decoder reads 8 bits, decodes them, and then reads another 8 bits. To ensure that the encoder can unambiguously interpret the variable length codes, you have to be careful how you assign these codes. Imagine that you were dealing with a four-character "alphabet" with four variable-length codes:
1. A: 1 2. B: 0 3. C: 10 4. D: 11
Example 2: Invalid variable-length code assignment
The problem with this assignment is that the codes are ambiguous. The decoder can't tell if the input sequence "10" is an A followed by a B, or a C by itself.
The solution is to assign prefix codes. With prefix codes, once you use a prefix to delineate a range of codes, it can't be used by itself as a code. So if the character "A" is assigned the 1-bit code "1", no other code can start with "1". If "B" is assigned the code "01", no other code can start with "01". A valid Huffman coding of the four-character alphabet above, then, is:
1. A: 1 2. B: 01 3. C: 001 4. D: 000
Example 3: Valid prefix-coding variable-length code assignment
This means that there can only be one 1-bit code, one two-bit code, two three-bit codes, four four-bit codes, etc. You may deal with prefix codes on a regular basis - the country calling codes that allow you to make international phone calls are assigned using prefix code rules. Prefix codes are usually referred to as Huffman codes [2] after the inventor of a provably optimal algorithm for generating them when symbol probabilities are known. These Huffman codes are often represented as trees, where each leaf is a symbol, and each branch is a bit value.
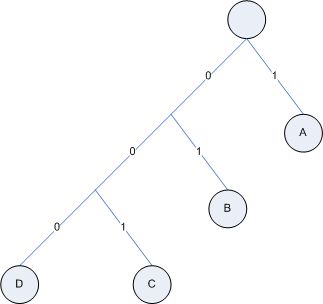
Figure 3: a prefix code tree
Once such a tree structure has been constructed, decoding is simple - start at the top of the tree and read in a bit of data. If the bit is a 0, follow the left-branch of the tree; if 1, follow the right-branch. When a leaf node is hit, stop; a symbol has been completely read. Output the symbol and return to the top of the tree.
Listing 1 illustrates a tree structure for representing Huffman codes in memory:
typedef struct huffman_node_t
{
int code; // -1 for non-leaf nodes
struct huffman_node_t *zero;
struct huffman_node_t *one;
}
huffman_node;
Listing 1: Huffman tree structure
Once constructed, reading these Huffman codes from an input stream is done as shown in listing 2:
huffman_node_t root;
build_huffman_tree( &root );
huffman_node_t node = &root;
while ( !eof )
{
if ( next_bit( stream ) )
{
node = node->one;
}
else
{
node = node->zero;
}
if ( node->code != -1 )
{
printf( "%c", node->code );
node = &root;
}
}
Listing 2: Decoding Huffman codes example
Any input sequence of these codes is completely unambiguous to the decoder. Notice that, in example 3, if the input consists mostly of C's and D's, then the output will be longer than the more straightforward canonical two-bit encoding of this four-character alphabet. On the other hand, if A's dominate, the input will be compressed. Therefore, by intelligently assigning Huffman codes to symbols - assigning high-frequency symbols to short code and low frequency symbols to longer codes - Huffman coding can, by itself, further compress the data.
GZIP mandates that the input first be LZ77 compressed, and that the LZ77 output itself be Huffman encoded so that the literals and pointers can be safely mixed together and still be decoded properly. Since different inputs will have different statistical distributions of symbols, the GZIP format requires that the compressed output specify a Huffman code table unique to the document before the actual compressed data. This Huffman code table is, itself, compressed - using more Huffman codes!
To make optimal use of space, the Deflate format [3] that GZIP depends on places additional constraints on the construction of the Huffman code table, so that the table can be completely specified by just outputting the lengths of each code. For instance, assume that there are 6 four-bit codes, 8 five-bit codes, and 12 six-bit codes. One simple way to ensure that each symbol can be decoded unambiguously, is to have the four-bit codes all begin with 0, the five-bit codes all begin with 10, and the six-bit codes all begin with 11. Therefore, the resulting Huffman table will look like:
0000: 0 0001: 1 0010: 2 0011: 3 0100: 4 0101: 5 0110: 6 10000: 7 10001: 8 10010: 9 10011: 10 10100: 11 10101: 12 10110: 13 10111: 14 110000: 15 110001: 16 110010: 17 110011: 18 110100: 19 110101: 20 110110: 21 110111: 22 111000: 23 111001: 24 111010: 25 111011: 26
Example 4: Simple reserved-prefix Huffman table
This can be extended to any number of bit-lengths - if there are seven-bit codes to be represented, then the six-bit codes will begin with 110, and the seven-bit codes will begin with 111. If there are eight-bit codes, then the six-bit codes will begin with 110, the seven-bit codes with 1110, and the eight-bit codes with 1111. Of course, this also means that there can only be 8 four-bit codes, 16 five-bit codes, etc.; in general, there can only be log2n-1 n-bit codes.
As it turns out, this approach to assigning variable length codes to symbols, although it's simple and it works, actually wastes a good part of the bit space. Consider the five-bit codes 01110 and 01111. In this example, there aren't any four bit codes that these can be confused with 0111 - since there are only six four-bit codes in this case. To make optimal use of the available bit space, then, the proper Huffman code assignment procedure is a bit different. Instead of prefix-coding everything, find the last code in the previous bit length, left-shift it by one (e.g. add a zero on the end), and start the next bit length from that value. So, following this scheme, the Huffman codes for the symbols described previously would be:
0000: 0 0001: 1 0010: 2 0011: 3 0100: 4 0101: 5 0110: 6 01110: 7 <- start a new sequence at (0110 + 1) << 1 01111: 8 10000: 9 10001: 10 10010: 11 10011: 12 10100: 13 10101: 14 101100: 15 <- start a new sequence at (10101 + 1) << 1 101101: 16 101110: 17 101111: 18 110000: 19 110001: 20 110010: 21 110011: 22 110100: 23 110101: 24 110110: 25 110111: 26
Example 5: More efficient Huffman code
Notice that there's no need for the codes to be assigned in order as in example 5 - the code for symbol 3 could be a six-bit code, and the code for symbol 20 could be a four-bit code. The only rule that needs to be followed is that the n-bit codes are assigned sequentially. So, if codes 2, 3, and 4 were six bits, and codes 19-21 were four bits, the Huffman table would be:
0000: 0 0001: 1 101100: 2 <- start a new sequence at (10101 + 1) << 1 101101: 3 101110: 4 0010: 5 <- pick up four-bit sequence where it left off 0011: 6 01110: 7 <- start a new sequence at (0110 + 1) << 1 01111: 8 10000: 9 10001: 10 10010: 11 10011: 12 10100: 13 10101: 14 101111: 15 <- pick up six-bit sequence where it left off 110000: 16 110001: 17 110010: 18 0100: 19 <- pick up four-bit sequence where it left off 0101: 20 0110: 21 110011: 22 <- pick up six-bit sequence where it left off 110100: 23 110101: 24 110110: 25 110111: 26
Example 6: Huffman code with interleaved bit lengths
Notice that the 6-bit sequence starts at the left-shifted value of one more than the last 5-bit sequence, even though the 5-bit sequences haven't been encountered yet.
By adopting this scheme, the encoder can just output the lengths of the codes, in order, and the decoder can reliably recreate the table in order to decode the compressed data that follows. Of course, the decoder has the easy part... it just needs to read the ranges and bit lengths to reconstruct the table. The encoder is responsible for assigning the high-frequency symbols to short codes, and the low-frequency symbols to longer codes to achieve optimal compression.
For a decoder to build a Huffman tree, then, all you need as input is a list of ranges and bit lengths. Define a new range structure as shown in listing 3:
typedef struct
{
int end;
int bit_length;
}
huffman_range;
Listing 3: Huffman Range structure
For example, you would describe the code tree in example 6 as shown in listing 4:
huffman_range range[ 7 ]; range[ 0 ].end = 1; range[ 0 ].bit_length = 4; range[ 1 ].end = 4; range[ 1 ].bit_length = 6; range[ 2 ].end = 6; range[ 2 ].bit_length = 4; range[ 3 ].end = 14; range[ 3 ].bit_length = 5; range[ 4 ].end = 18; range[ 4 ].bit_length = 6; range[ 5 ].end = 21; range[ 5 ].bit_length = 4; range[ 6 ].end = 26; range[ 6 ].bit_length = 6;
Listing 4: Describing a Huffman tree using symbols and bit lengths
Once these ranges are defined, building the Huffman tree, following the rules described above, is done as described in RFC 1951.
typedef struct
{
unsigned int len;
unsigned int code;
}
tree_node;
static void build_huffman_tree( huffman_node *root,
int range_len,
huffman_range *range )
{
int *bl_count;
int *next_code;
tree_node *tree;
int bits;
int code = 0;
int n;
int active_range;
int max_bit_length;
max_bit_length = 0;
for ( n = 0; n < range_len; n++ )
{
if ( range[ n ].bit_length > max_bit_length )
{
max_bit_length = range[ n ].bit_length;
}
}
Listing 5: Determine the maximum bit length
bl_count = malloc( sizeof( int ) * ( max_bit_length + 1 ) ); next_code = malloc( sizeof( int ) * ( max_bit_length + 1 ) ); tree = malloc( sizeof( tree_node ) * ( range[ range_len - 1 ].end + 1 ) );
Listing 6: Allocate space for work areas
memset( bl_count, '\0', sizeof( int ) * ( max_bit_length + 1 ) );
for ( n = 0; n < range_len; n++ )
{
bl_count[ range[ n ].bit_length ] +=
range[ n ].end - ( ( n > 0 ) ? range[ n - 1 ].end : -1 );
}
Listing 7: Determine bit length counts
// step 2, directly from RFC
memset( next_code, '\0', sizeof( int ) * ( max_bit_length + 1 ) );
for ( bits = 1; bits <= max_bit_length; bits++ )
{
code = ( code + bl_count[ bits - 1 ] ) << 1;
if ( bl_count[ bits ] )
{
next_code[ bits ] = code;
}
}
Listing 8: Determine the first code of each bit length
// step 3, directly from RFC
memset( tree, '\0', sizeof( tree_node ) *
( range[ range_len - 1 ].end + 1 ) );
active_range = 0;
for ( n = 0; n <= range[ range_len - 1 ].end; n++ )
{
if ( n > range[ active_range ].end )
{
active_range++;
}
if ( range[ active_range ].bit_length )
{
tree[ n ].len = range[ active_range ].bit_length;
if ( tree[ n ].len != 0 )
{
tree[ n ].code = next_code[ tree[ n ].len ];
next_code[ tree[ n ].len ]++;
}
}
}
Listing 9: Build the code table
root->code = -1;
for ( n = 0; n <= range[ range_len - 1 ].end; n++ )
{
huffman_node *node;
node = root;
if ( tree[ n ].len )
{
for ( bits = tree[ n ].len; bits; bits-- )
{
if ( tree[ n ].code & ( 1 << ( bits - 1 ) ) )
{
if ( !node->one )
{
node->one = ( struct huffman_node_t * )
malloc( sizeof( huffman_node ) );
memset( node->one, '\0', sizeof( huffman_node ) );
node->one->code = -1;
}
node = ( huffman_node * ) node->one;
}
else
{
if ( !node->zero )
{
node->zero = ( struct huffman_node_t * )
malloc( sizeof( huffman_node ) );
memset( node->zero, '\0', sizeof( huffman_node ) );
node->zero->code = -1;
}
node = ( huffman_node * ) node->zero;
}
}
assert( node->code == -1 );
node->code = n;
}
}
free( bl_count );
free( next_code );
free( tree );
}
Listing 10: Turn the code table into a tree structure and free allocated memory
However, the Huffman code table itself is pretty big. It has to include codes for all 255 possible literal bytes, as well as the back pointers themselves. As a result, the lengths of the codes are themselves Huffman encoded! To avoid conceptual infinite recursion, the lengths of those codes are not Huffman encoded, but instead given as fixed three-bit fields. This means that there can only be at most 8 unique length codes for the Huffman codes that represent the compressed data itself. To summarize, then, the Deflate format is illustrated in figure 4: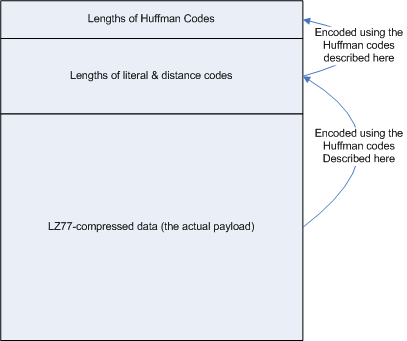
Figure 4: DEFLATE format
The job of the decoder, then, at a high level, is:
There's actually one more bit of "header" data that precedes even the lengths of the Huffman codes - a set of fixed-length declarations that describe how many Huffman codes follow, to allow interpretation of the two tables of Huffman code lengths that follow.
Before continuing, though, I need to describe exactly how GZIP packs bits into bytes. Rather than packing bits into bytes linearly, GZIP has a strange formulation where the bits themselves are read LSB to MSB as illustrated in figure 6:
<---- 87654321
Figure 6: GZIP bit ordering
This isn't strange by itself - this is just little-endian ordering (Intel-based processors do this by default). However, the contents themselves are interpreted in big-endian format! So, a five-bit code followed by a three-bit code would be packed into a single 8-bit byte as in figure 7:
<-- 12312345
Figure 7: two packed values
If codes cross byte boundaries (which is the rule rather than the exception for variable-length codes), the bytes themselves should be read sequentially (of course), but interpreting the bits within them is still done right-to-left, but then reversed for interpretation. For instance, a 6-bit code followed by a 5-bit code followed by a 3-bit code would be streamed as the two bytes show in figure 8:
<--- <--- xx123123 45123456
Figure 8: three packed values, crossing a byte boundary
All of this is fairly confusing, but fortunately you can hide the complexity in a few convenience routines. Since you'll be reading the input from file, define a new wrapper structure named "bit_stream" as shown in listing 11:
typedef struct
{
FILE *source;
unsigned char buf;
unsigned char mask; // current bit position within buf; 8 is MSB
}
bit_stream;
Listing 11: bit_stream declaration
Now define a convenience routine to read the data from the stream bit-by-bit, LSB to MSB as shown in listing 12:
unsigned int next_bit( bit_stream *stream )
{
unsigned int bit = 0;
bit = ( stream->buf & stream->mask ) ? 1 : 0;
stream->mask <<= 1;
if ( !stream->mask )
{
stream->mask = 0x01;
if ( fread( &stream->buf, 1, 1, stream->source ) < 1 )
{
perror( "Error reading compressed input" );
// TODO abort here?
}
}
return bit;
}
Listing 12: next_bit function
Finally, since the bits should be read in little-endian form but interpreted in big-endian form, define a convenience method to read the bits but then turn around and invert them for interpretation as shown in listing 13:
int read_bits_inv( bit_stream *stream, int count )
{
int bits_value = 0;
int i = 0;
int bit;
for ( i = 0; i < count; i++ )
{
bit = next_bit( stream );
bits_value |= ( bit << i );
}
return bits_value;
}
Listing 13: Read bits and invert
Now you can start actually reading in compressed data. The first section of a GZIP-compressed block is three integers indicating the number of length codes, the number of literal codes, and the number of distance codes.
static void read_huffman_tree( bit_stream *stream )
{
int hlit;
int hdist;
int hclen;
hlit = read_bits_inv( stream, 5 );
hdist = read_bits_inv( stream, 5 );
hclen = read_bits_inv( stream, 4 );
Listing 14: Read the GZIP pre-header
hclen is the declaration of four less than how many 3-bit length codes follow. These length codes define a Huffman tree - after the 3-bit length codes, there are 257 + hdist + hlit literal and distance length codes, encoded using this Huffman tree.
Attachment #1 is a gzipped input file (it's the gzipped representation of the source code for this article). It declares hlit = 23, hdist = 27, hclen = 8. This means that, immediately following the pre-header, there are ( 8 + 4 ) * 3 = 36 bits of code lengths bits. This pre-header describes a Huffman tree that describes how to interpret 257 + hdist + hlit codes that follow. These codes are the ones that describe both the literals, distance and length codes that actually comprise the gzipped payload.
Where does the magic number 257 come from? Well, that's 255 literal codes (the 8-bit input range), one "stop" code, and at least one length code (if there isn't at least one length code, then there's no point in applying LZ77 in the first place). However, even Huffman-encoded, 255 literal codes is quite a few, especially considering that many input documents will not include every possible 8-bit combination of input bytes. For instance, ASCII-coded text will not include any input bytes greater than 128. For space efficiency, then, it's necessary to make it easy to exclude long ranges of the input space and not use up a Huffman code on literals that will never appear.
So, the Huffman code lengths that follow the code length bits can fall into two separate categories. The first is a literal length - declaring, for instance, that the Huffman code for the literal byte '32' is 9 bits long. The second category is a run-length declaration; this tells the decoder that either the previous code, or the value "0" (indicating that the given literal never appears in the gzipped document), occurs multiple times. This method of using a single value to indicate multiple consecutive values in the data is a third compression technique, referred to as "run-length-encoding" [4]. Therefore, the hclen code length bits that follow the pre-header are either length codes, or repetition codes. The specification refers to the repetition codes as the values 16, 17, and 18, but these numbers don't have any real physical meaning - 16 means "repeat the previous character n times", and 17 & 18 mean "insert n 0's". The number n follows the repeat codes and is encoded (without compression) in 2, 3 or 7 bits, respectively.
To make this all just a little bit more confusing - these length codes are given out of order. The first code given isn't the code for the length '0'; it's actually the code for "repeat the previous character n times" (16). This is followed by 17 and 18, then 0, 8, 7, 9, 6, 10, 5, 11, 4, 12, 3, 13, 2, 14, 1 and finally 15. Why the schizophrenic order? Because codes of lengths 15, 1, 14 and 2 are likely to be very rare in real-world data - the codes themselves are given in order of expected frequency. This way, if the literal and distance code tables that follow don't have any codes of length 1, there's no need to even declare them. In fact, if you notice, attachment 1 only declares 11 code length codes - this means that codes of length 12, 3, 13, 2, 14, 1 and 15 just don't occur in the following table, so there's no need to waste output space declaring them. After all, a 15-bit code would have to almost never occur in order to be space efficient; a 1-bit code would have to occur in almost every position for the encoding to be worth using up a whole prefix for a single value.
This whole process probably seems a little abstract at this point - hopefully an example will help clear things up. Attachment #1 starts with the fixed 14-bit pre-header:
11101110110001 hlit|hdist|hclen 11101 hlit = 23 11011 hdist = 27 0001 hclen = 8
Remember that the bits are read left-to-right, but then swapped before interpretation, so they appear in little-endian form. This declares that there follows 36 ( (8 + 4) * 3 ) bits of code length declarations. These appear as:
110111111011011010011001100100101100
| 110 | 111 | 111 | 011 | 011 | 010 | 011 | 001 | 100 | 100 | 101 | 100 |
| 16 | 17 | 18 | 0 | 8 | 7 | 9 | 6 | 10 | 5 | 11 | 4 |
| 6 | 7 | 7 | 3 | 3 | 2 | 3 | 3 | 4 | 4 | 5 | 4 |
This needs to be turned into a Huffman tree in order to interpret the codes that follow, using the build_huffman_tree function declared in listings 5 - 10. To do that, a range must be built - in this case, it is:
| range end | bit length |
|---|---|
| 0 | 3 |
| 1-3 | 0 |
| 4-5 | 4 |
| 6 | 3 |
| 7 | 2 |
| 8-9 | 3 |
| 10 | 4 |
| 11 | 5 |
| 12-15 | 0 |
| 16 | 6 |
| 17-18 | 7 |
Where a bit-length of 0 indicates that the length doesn't occur in the table that follows. Following the rules of Huffman codes described above, this works out to the Huffman tree:
010: 0 1100: 4 1101: 5 011: 6 00: 7 100: 8 101: 9 1110: 10 11110: 11 111110: 16 1111110: 17 1111111: 18
Table 1: Attachment #1 code lengths Huffman tree
What this means is that, in the data that follows, two consecutive zero bits indicates a value of 7. 1100 indicates a value of 4, etc. You might want to work through this to make sure you understand how the range table converts to the Huffman table before continuing.
Listing 15 illustrates how to read this first part of the deflated input and build a Huffman tree from it.
static void read_huffman_tree( bit_stream *stream )
{
int hlit;
int hdist;
int hclen;
int i, j;
int code_lengths[ 19 ];
huffman_node code_lengths_root;
huffman_range code_length_ranges[ 19 ];
static int code_length_offsets[] = {
16, 17, 18, 0, 8, 7, 9, 6, 10, 5, 11, 4, 12, 3, 13, 2, 14, 1, 15 };
hlit = read_bits_inv( stream, 5 );
hdist = read_bits_inv( stream, 5 );
hclen = read_bits_inv( stream, 4 );
memset( code_lengths, '\0', sizeof( code_lengths ) );
for ( i = 0; i < ( hclen + 4 ); i++ )
{
code_lengths[ code_length_offsets[ i ] ] = read_bits_inv( stream, 3 );
}
// Turn those into actionable ranges for the huffman tree routine
j = 0; // j becomes the length of the range array
for ( i = 0; i < 19; i++ )
{
if ( ( i > 0 ) && ( code_lengths[ i ] != code_lengths[ i - 1 ] ) )
{
j++;
}
code_length_ranges[ j ].end = i;
code_length_ranges[ j ].bit_length = code_lengths[ i ];
}
memset( &code_lengths_root, '\0', sizeof( huffman_node ) );
build_huffman_tree( &code_lengths_root, j + 1, code_length_ranges );
Listing 15: Building the code lengths Huffman tree
After this runs, code_lengths_root will point to the root of a Huffman tree that can be used to interpret the next part of the input data, until 257 + hlit + hdist data values have been input. Remember that the codes for 16, 17 and 18 (Huffman codes 11110, 111110, 111111 in this example) indicate repetition, so there won't necessarily be 257 + hlit + hdist Huffman-coded values, if repetition codes are used (which they almost always are).
Even Huffman and run-length encoded, the table that follows is large - in attachment #1, there are 139 codes that represent 307 (257 + 23 + 27) length codes. I won't reproduce the whole thing here, but I'll illustrate the first few values, so you can see how it's interpreted. The beginning of the table is:
11111011101011111101010001101100011100...
Interpreting this via the Huffman table decoded in table #1, you see this works out to:
| 1111110 | 111 | 00 | 1111111 | 0101000 | 1101 | 101 | 100 | 1110 |
| 17 | repeat 10 | 7 | 18 | repeat 21 | 5 | 9 | 8 | 10 |
(Aside: why 11? That's the longest number that can be encoded using the repeat count declarator 17, which is followed by a 3-bit count to which 3 is added).
Next is 5, 9, 8 and 10. So, the first 35 bit lengths are:
1 2 3 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 ... 0 0 0 0 0 0 0 0 0 0 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5 9 8 10 ...
These bit lengths will be used to generate another Huffman table. The first 255 codes in this array are the literal bytes, which appeared in the input that was supplied to the LZ77 compression algorithm in the first place. This is followed by the special "stop" code and up to 30 length declarators, indicating backpointers. Finally, there will be up to 32 distance code lengths.
To interpret the whole thing and build a couple of Huffman trees from them - one for literal/length codes and another for distance codes, see listing 16, which is a modified version of listing 15. Note that the input has changed to pass the literal/length and distance code Huffman trees back to the caller; the caller is expected to use these trees to interpret the remainder of the input file.
static void read_huffman_tree( bit_stream *stream,
huffman_node *literals_root,
huffman_node *distances_root )
{
huffman_range code_length_ranges[ 18 ];
int *alphabet;
huffman_range *alphabet_ranges;
huffman_node code_lengths_root;
huffman_node *code_lengths_node;
...
build_huffman_tree( &code_lengths_root, j + 1, code_length_ranges );
// read the literal/length alphabet; this is encoded using the huffman
// tree from the previous step
i = 0;
alphabet = ( int * ) malloc( ( hlit + hdist + 258 ) * sizeof( int ) );
alphabet_ranges = ( huffman_range * ) malloc( ( hlit + hdist + 258 ) *
sizeof( huffman_range ) );
code_lengths_node = &code_lengths_root;
while ( i < ( hlit + hdist + 258 ) )
{
if ( next_bit( stream ) )
{
code_lengths_node = code_lengths_node->one;
}
else
{
code_lengths_node = code_lengths_node->zero;
}
if ( code_lengths_node->code != -1 )
{
if ( code_lengths_node->code > 15 )
{
int repeat_length;
switch ( code_lengths_node->code )
{
case 16:
repeat_length = read_bits_inv( stream, 2 ) + 3;
break;
case 17:
repeat_length = read_bits_inv( stream, 3 ) + 3;
break;
case 18:
repeat_length = read_bits_inv( stream, 7 ) + 11;
break;
}
while ( repeat_length-- )
{
if ( code_lengths_node->code == 16 )
{
alphabet[ i ] = alphabet[ i - 1 ];
}
else
{
alphabet[ i ] = 0;
}
i++;
}
}
else
{
alphabet[ i ] = code_lengths_node->code;
i++;
}
code_lengths_node = &code_lengths_root;
}
}
// Ok, now the alphabet lengths have been read. Turn _those_
// into a valid range declaration and build the final huffman
// code from it.
j = 0;
for ( i = 0; i <= ( hlit + 257 ); i++ )
{
if ( ( i > 0 ) && ( alphabet[ i ] != alphabet[ i - 1 ] ) )
{
j++;
}
alphabet_ranges[ j ].end = i;
alphabet_ranges[ j ].bit_length = alphabet[ i ];
}
build_huffman_tree( literals_root, j, alphabet_ranges );
i--;
j = 0;
for ( ; i <= ( hdist + hlit + 258 ); i++ )
{
if ( ( i > ( 257 + hlit ) ) && ( alphabet[ i ] != alphabet[ i - 1 ] ) )
{
j++;
}
alphabet_ranges[ j ].end = i - ( 257 + hlit );
alphabet_ranges[ j ].bit_length = alphabet[ i ];
}
build_huffman_tree( distances_root, j, alphabet_ranges );
free( alphabet );
free( alphabet_ranges );
}
Listing 16: Read the literal/length and distance code Huffman trees
This is a bit dense, but implements the logic for using the code lengths Huffman tree to build two new Huffman trees which can then be used to decode the final LZ77-compressed data.
The process of actually reading the compressed data involves first interpreting a Huffman code according to the literal/length table. Check to see if it's a literal (e.g. < 256) and if so, output it. If it's the stop code (e.g. = 256), stop. If it's a length code (e.g. > 256), it's a backpointer.
Interpreting backpointers is the most complex part of inflating gzipped input. Similar to the "sliding scales" that were used by the code lengths Huffman tree, where a 17 was followed by three bits indicating the actual length and 18 was followed by 7 bits, different length codes are followed by variable numbers of extra bits. If the length code is between 257 and 264, subtract 254 from it - this is the length of the backpointed range, without any extra length bits. However, if the length code is in the range 265 to 285, it's followed by ( code - 261 ) / 4 bits of extra data which indicate a length. These bits are then added to another code (whose value depends on the length code itself) to get the actual length of the range. In this way, very large backpointers can be represented, but the common cases of short lengths can be coded efficiently.
A length code is always followed by a distance code, indicating how far back in the input buffer the matched range was found. Distance codes allow for extra bits just like length codes do - the distance code values 0-3 are literally matched, while the remaining 28 are followed by ( code - 2 ) / 2 bits of extra data, to which a variable number is added. The lengths codes can range from 3-258, but the distance codes can range from 1-32768 - which means that, while decompressing, it's necessary to keep track of at least the previous 32,768 input characters.
Listing 17 illustrates how to use the literal/length and distance Huffman trees to interpret and decompress LZ77-compressed data from a bit stream.
#define MAX_DISTANCE 32768
static int inflate_huffman_codes( bit_stream *stream,
huffman_node *literals_root,
huffman_node *distances_root )
{
huffman_node *node;
int stop_code = 0;
unsigned char buf[ MAX_DISTANCE ];
unsigned char *ptr = buf;
int extra_length_addend[] = {
11, 13, 15, 17, 19, 23, 27,
31, 35, 43, 51, 59, 67, 83,
99, 115, 131, 163, 195, 227
};
int extra_dist_addend[] = {
4, 6, 8, 12, 16, 24, 32, 48,
64, 96, 128, 192, 256, 384,
512, 768, 1024, 1536, 2048,
3072, 4096, 6144, 8192,
12288, 16384, 24576
};
node = literals_root;
while ( !stop_code )
{
if ( feof( stream->source ) )
{
fprintf( stderr, "Premature end of file.\n" );
return 1;
}
if ( next_bit( stream ) )
{
node = node->one;
}
else
{
node = node->zero;
}
if ( node->code != -1 )
{
// Found a leaf in the tree; decode a symbol
assert( node->code < 286 ); // should never happen
// leaf node; output it
if ( node->code < 256 )
{
*(ptr++) = node->code;
}
if ( node->code == 256 )
{
stop_code = 1;
break;
}
if ( node->code > 256 )
{
int length;
int dist;
int extra_bits;
// This is a back-pointer to a position in the stream
// Interpret the length here as specified in 3.2.5
if ( node->code < 265 )
{
length = node->code - 254;
}
else
{
if ( node->code < 285 )
{
extra_bits = read_bits_inv( stream, ( node->code - 261 ) / 4 );
length = extra_bits + extra_length_addend[ node->code - 265 ];
}
else
{
length = 258;
}
}
// The length is followed by the distance.
// The distance is coded in 5 bits, and may be
// followed by extra bits as specified in 3.2.5
node = distances_root;
while ( node->code == -1 )
{
if ( next_bit( stream ) )
{
node = node->one;
}
else
{
node = node->zero;
}
}
dist = node->code;
if ( dist > 3 )
{
int extra_dist = read_bits_inv( stream, ( dist - 2 ) / 2 );
dist = extra_dist + extra_dist_addend[ dist - 4 ];
}
// TODO change buf into a circular array so that it
// can handle files of size > 32768 bytes
{
unsigned char *backptr = ptr - dist - 1;
while ( length-- )
{
// Note that ptr & backptr can overlap
*(ptr++) = *(backptr++);
}
}
}
node = literals_root;
}
}
*ptr = '\0';
printf( "%s\n", buf );
return 0;
}
Listing 17: Inflating Huffman-encoded LZ77-compressed input
Listing 17 should be fairly straightforward to understand at this point - read Huffman codes, one after another, and interpret them as literals or backpointers as described previously. Note that this routine, as implemented, can't decode more than 32768 bytes of output, and that it assumes that the output is ASCII-formatted text. A more general-purpose gunzip routine would handle larger volumes of data and would return the result back to the caller for interpretation.
If you've made it this far, you're through the hard parts. Everything else involved in unzipping a gzipped file is boilerplate. A gzipped file starts with a header that first declares it as a gzipped file and declares some metadata about the file itself. Describe a couple of structures to house this data as shown in listing 18:
typedef struct
{
unsigned char id[ 2 ];
unsigned char compression_method;
unsigned char flags;
unsigned char mtime[ 4 ];
unsigned char extra_flags;
unsigned char os;
}
gzip_header;
typedef struct
{
gzip_header header;
unsigned short xlen;
unsigned char *extra;
unsigned char *fname;
unsigned char *fcomment;
unsigned short crc16;
}
gzip_file;
Listing 18: The top-level gzip file structure
Go ahead and declare a main routine as shown in listing 19 that expects to be passed in the name of a gzipped file, and will read the header and output some of its metadata.
#define FTEXT 0x01
#define FHCRC 0x02
#define FEXTRA 0x04
#define FNAME 0x08
#define FCOMMENT 0x10
int main( int argc, char *argv[ ] )
{
FILE *in;
gzip_file gzip;
gzip.extra = NULL;
gzip.fname = NULL;
gzip.fcomment = NULL;
if ( argc < 2 )
{
fprintf( stderr, "Usage: %s <gzipped input file>\n", argv[ 0 ] );
exit( 1 );
}
in = fopen( argv[ 1 ], "r" );
if ( !in )
{
fprintf( stderr, "Unable to open file '%s' for reading.\n", argv[ 1 ] );
exit( 1 );
}
if ( fread( &gzip.header, sizeof( gzip_header ), 1, in ) < 1 )
{
perror( "Error reading header" );
goto done;
}
if ( ( gzip.header.id[ 0 ] != 0x1f ) || ( gzip.header.id[ 1 ] != 0x8b ) )
{
fprintf( stderr, "Input not in gzip format.\n" );
goto done;
}
if ( gzip.header.compression_method != 8 )
{
fprintf( stderr, "Unrecognized compression method.\n" );
goto done;
}
if ( gzip.header.flags & FEXTRA )
{
// TODO spec seems to indicate that this is little-endian;
// htons for big-endian machines?
if ( fread( &gzip.xlen, 2, 1, in ) < 1 )
{
perror( "Error reading extras length" );
goto done;
}
gzip.extra = ( unsigned char * ) malloc( gzip.xlen );
if ( fread( gzip.extra, gzip.xlen, 1, in ) < 1 )
{
perror( "Error reading extras" );
goto done;
}
// TODO interpret the extra data
}
if ( gzip.header.flags & FNAME )
{
if ( read_string( in, &gzip.fname ) )
{
goto done;
}
}
if ( gzip.header.flags & FCOMMENT )
{
if ( read_string( in, &gzip.fcomment ) )
{
goto done;
}
}
if ( gzip.header.flags & FHCRC )
{
if ( fread( &gzip.crc16, 2, 1, in ) < 1 )
{
perror( "Error reading CRC16" );
goto done;
}
}
...
Listing 19: main routine to strip off the GZIP header
I won't go over this in detail; refer to RFC 1952 [5] if you want more specifics. Note that a gzip file must begin with the magic bytes 1F8B, or it's not considered a valid gzipped file. Also note that a gzipped file can be prepended with an optional original filename and/or a comment - these are given in null-terminated ASCII form. Finally, the header can optionally be protected by a CRC16, although this is rare.
Once the header is read, the compressed data, as described by the routines above, follows. However, there's one extra layer of header metadata. A gzipped file actual consists of multiple blocks of deflated data (usually there's just one block, but the file format permits more than one). The blocks themselves can either be uncompressed or compressed according to the deflate specification described previously. Also, in a nod to space efficiency, very small inputs can use a boilerplate set of Huffman codes, and not declare their own Huffman tables at all. This way, if the compressed data is actually larger than the original input when the Huffman tables are included, the data can be reasonably compressed.
The GZIP file format, then, after the standard header, consists of a series of blocks. The block format is a single bit indicating whether or not this block is the last block (1 = yes, 0 = no), and two bits indicating the block type: 00 = uncompressed, 01 = compressed using fixed Huffman codes, 10 = compressed using declared dynamic Huffman codes (11 is an invalid block type). Listing 20 illustrates the final inflate routine that reads the block type and calls the appropriate inflation routine:
static int inflate( FILE *compressed_input )
{
// bit 8 set indicates that this is the last block
// bits 7 & 6 indicate compression type
unsigned char block_format;
bit_stream stream;
int last_block;
huffman_node literals_root;
huffman_node distances_root;
stream.source = compressed_input;
fread( &stream.buf, 1, 1, compressed_input );
stream.mask = 0x01;
do
{
last_block = next_bit( &stream );
block_format = read_bits_inv( &stream, 2 );
switch ( block_format )
{
case 0x00:
fprintf( stderr, "uncompressed block type not supported.\n" );
return 1;
break;
case 0x01:
memset( &literals_root, '\0', sizeof( huffman_node ) );
build_fixed_huffman_tree( &literals_root );
inflate_huffman_codes( &stream, &literals_root, NULL );
break;
case 0x02:
memset( &literals_root, '\0', sizeof( huffman_node ) );
memset( &distances_root, '\0', sizeof( huffman_node ) );
read_huffman_tree( &stream, &literals_root, &distances_root );
inflate_huffman_codes( &stream, &literals_root, &distances_root );
break;
default:
fprintf( stderr, "Error, unsupported block type %x.\n", block_format );
return 1;
}
}
while ( !last_block );
return 0;
}
Listing 20: inflating multiple blocks
Notice that the bit stream declared in listing 11 is initialized here. The read_huffman_tree from listing 16 is called if the block type is 10, and inflate_huffman_codes from listing 17 is called in either case to actually deflate the data.
The only new routine here is build_fixed_huffman_tree, and is shown in listing 21:
static void build_fixed_huffman_tree( huffman_node *root )
{
huffman_range range[ 4 ];
range[ 0 ].end = 143;
range[ 0 ].bit_length = 8;
range[ 1 ].end = 255;
range[ 1 ].bit_length = 9;
range[ 2 ].end = 279;
range[ 2 ].bit_length = 7;
range[ 3 ].end = 287;
range[ 3 ].bit_length = 8;
build_huffman_tree( root, 4, range );
}
Listing 21: Build fixed Huffman tree
As you can imagine, this fixed Huffman tree isn't optimal for any input data set, but if the input is small (less than a few hundred bytes), it's better to use this less efficient Huffman tree to encode the literals and lengths than to use up potentially a few hundred bytes declaring a more targeted Huffman tree. Notice also that there's no distance tree - when fixed Huffman trees are used, the distances are always specified in five bits, not coded. To support this, make the small change in listing 22 to the inflate_huffman_codes routine:
else
{
length = 258;
}
}
// The length is followed by the distance.
// The distance is coded in 5 bits.
if ( distances_root == NULL )
{
// Hardcoded distances
dist = read_bits_inv( stream, 5 );
}
else
{
// dynamic distances
node = distances_root;
while ( node->code == -1 )
{
if ( next_bit( stream ) )
{
node = node->one;
}
else
{
node = node->zero;
}
}
dist = node->code;
}
Listing 22: Supporting hardcoded distances in inflate_huffman_codes
Notice that the hardcoded distances are still subject to "extra bit" interpretation just like the dynamic ones are.
That's almost it. Insert a call to "inflate" at the end of the main routine as shown in listing 23:
if ( gzip.header.flags & FHCRC )
{
if ( fread( &gzip.crc16, 2, 1, in ) < 1 )
{
perror( "Error reading CRC16" );
goto done;
}
}
if ( inflate( in ) )
{
goto done;
}
Listing 23: call the inflate routine
In fact, that could be it - except that there's a small problem with compressing data. With uncompressed data, one bit error affects at best one byte, and at worst a contiguous chunk of data - but a flipped bit in uncompressed data doesn't render the whole document unreadable. Compressed data, due to it's natural push to make the most efficient use of space down to the bit level, is highly susceptible to minor errors. A single bit flipped in transmission will change the meaning of the entire remainder of the document. Although bit-flipping errors are rarer and rarer on modern hardware, you still want some assurance that what you decompressed was what the author compressed in the first place. Whereas with ASCII text, it's obvious to a human reader that the data didn't decompress correctly if an error occurs, imagine a binary document that represents, for instance, weather meter readings. The readings can range from 0-255 and vary wildly; if the document uncompressed incorrectly, the reader would have no way to detect the error.
Therefore, GZIP mandates that each document end with a standard trailer that consists of a Cyclic Redundancy Check (CRC) and the length of the uncompressed data. The decompressor can compare both to the output and verify that they're correct before blessing the document as correctly inflated.
A CRC is sort of like a checksum, but a more reliable one. A checksum is a simple mechanism to give the receiver some assurance that what was sent is what was received - the concept is to sum all of the input bytes modulo an agreed-upon base (typically 232) and transmit the resulting sum. This is simple for each side to quickly compute, and if either side disagrees on the result, something has gone wrong during transmission.
However, checksums aren't optimal when it comes to detecting bit errors. If a single bit is flipped, then the checksums won't match, as you would want. However, if two bits are flipped, it's possible that they can flip in such a way as to cancel each other out, and the checksum won't detect the error. The CRC, developed in W. Peterson in 1961 [6], is a more robust check mechanism which is less susceptible to this error cancellation.
In a future installment of this series, I'll cover the CRC32 value and add support for CRC32 validation to the gunzip routine presented here. However, I'd encourage you to download the source code and use it to decompress a few small documents and step through the code to see if you can understand what's going on and how it all works. Of course, if you want to do any real decompression, use a real tool such as GNU Gunzip. However, I've found the utility described here very helpful in understanding how the algorithm works and how GZIP compression goes about doing its job.
I believe that the code in this article is free from errors, but I haven't tested it extensively - please, whatever you do, don't use it in a production environment (use GNU gzip instead!) However, if you do spot an error, please let me know about it.
References: